机器学习在量化研究中的应用 / Notes 丨 Milvoid's Journal

Partially Generanted with ChatGPT

回归法

1. 什么是因子？

因子（Factor）是指能够解释或预测资产收益、风险或其他特性的一种量化指标。在金融研究中，因子是基于理论或经验得出的变量，用来捕捉资产收益的系统性驱动因素。简单来说，因子是一种假设资产表现的关键影响变量。

因子的类型

因子可以分为以下几类：

宏观因子：
- 表示市场或经济的整体特征。
- 示例：利率水平、GDP 增速、通胀率。
微观因子：
- 表示单个资产的特性。
- 示例：市值（Size）、账面市值比（Book-to-Market）、动量（Momentum）。
技术因子：
- 从价格、交易量等市场数据衍生的指标。
- 示例：移动平均线、RSI 指标。
风格因子：
- 表示资产所属的某种风格。
- 示例：成长因子（Growth）、价值因子（Value）。

因子的典型数据类型

因子通常是数值型变量，通常在时间和资产的交叉面上定义。它们的数据类型包括：

数值型（连续变量）：例如动量因子（某个时间段内的收益率）。
分类型（离散变量）：例如行业因子（行业分类编码）。

2. 回归方程的含义

回归方程的核心在于表达 资产收益与因子的关系。它试图从数学角度回答以下问题：

收益的驱动力是什么？
哪些因子能够解释收益的变化？
因子的边际贡献如何？

单因子回归方程

单因子回归的形式为：

$r_i = \alpha + \beta F_i + \epsilon$

$ r_i $ ：资产 $ i $ 的收益率，通常是未来某个时间段的收益率。
$ F_i $ ：因子值，代表资产 $ i $ 在某个时间点的特性。
$ \alpha $ ：回归截距，表示在因子对收益没有影响时的收益水平。
$ \beta $ ：回归系数，表示因子值每变化一个单位对资产收益的影响。
$ \epsilon $ ：残差项，表示收益中未被因子解释的部分。

解释：

如果 $ \beta $ 显著为正，说明因子 $ F $ 对资产收益有正向影响。
如果 $ \beta $ 显著为负，说明因子 $ F $ 对资产收益有负向影响。

多因子回归方程

引入多个因子后的回归模型为：

$r_i = \alpha + \beta_1 F_{1i} + \beta_2 F_{2i} + \ldots + \beta_k F_{ki} + \epsilon$

$ F{1i}, F{2i}, \ldots, F_{ki} $ ：表示 $ i $ 资产的不同因子值。
$ \beta_1, \beta_2, \ldots, \beta_k $ ：每个因子的系数，衡量每个因子对收益的边际贡献。

3. 使用回归方程的目的

回归模型在因子分析中的主要应用包括以下几个方面：

(1) 验证因子是否有效

通过回归模型，可以检验因子是否能够显著解释资产收益。如果回归系数（ $ \beta $ ）显著不为零，说明因子对收益有解释力。

目的：判断因子是否有预测能力。

(2) 衡量因子的强弱

回归系数（ $ \beta $ ）的大小表明因子的影响程度。较大的系数表明该因子对收益的影响更强。

目的：筛选强因子。

(3) 分析因子组合的独立性

在多因子模型中，可以检查因子间的独立性。如果两个因子高度相关（共线性），需要进一步处理（如因子正交化）。

目的：提高因子组合的多样性和有效性。

(4) 风险暴露分析

回归模型可以用于分析资产对各个风险因子的暴露程度，从而用于构建风险对冲策略。

目的：管理组合的风险敞口。

(5) 因子投资组合构建

利用因子回归模型，可以根据因子值构建投资组合。例如，买入高因子值资产、卖出低因子值资产，形成因子对冲组合。

目的：构建因子驱动的超额收益策略。

总结

因子是资产收益的驱动变量，而回归模型为我们提供了一种量化分析因子效果的工具。通过回归方程，我们可以：

验证因子的有效性。
衡量因子的强弱。
构建因子组合。
管理风险敞口。

这不仅是评估因子质量的核心步骤，也是将因子应用于投资实践的基础。你对其中的哪个具体环节有兴趣，我可以深入探讨！

1. 回归法的基本思想

回归法通常用来测试因子是否对股票收益具有解释力，同时可以评估因子与其他因子之间的相关性或独立性。

回归方程：

其中：
- $ r_i $ ：第 $ i $ 个资产的超额收益。
- $ F $ ：研究的因子值。
- $ \alpha $ ：截距项。
- $ \beta $ ：因子的系数，衡量因子对收益的影响。
- $ \epsilon $ ：回归残差，表示无法被因子解释的部分。

回归法的目标是检验因子 $ F $ 的显著性（例如， $ \beta $ 是否显著不为 0），并计算解释力（如 $ R^2 $ ）。

2. 因子质量的评估指标

通过回归法，可以通过以下几个指标评估因子质量：

(1) 显著性检验

对回归系数 $ \beta $ 做 t 检验。
如果因子的 t 值显著（通常 $ t > 2 $ 或 $ p < 0.05 $ ），说明因子对收益的解释能力显著。

(2) 因子的解释力

$ R^2 $ （决定系数）：衡量因子对收益波动的解释程度。
$ Adjusted\ R^2 $ ：调整后的 $ R^2 $ ，更适合多因子回归模型。

(3) 独立性检验

检查因子是否与其他因子显著相关。例如，通过加入多个因子进行多元回归，检验因子的边际解释能力。
如果某因子显著但与其他因子高度相关，可能存在冗余。

(4) 信息系数（IC, Information Coefficient）

计算因子值与未来收益之间的相关性（通常用 Spearman 秩相关系数）。
高的 IC 值表明因子对未来收益有预测能力。

3. 回归法的实践步骤

以下是回归法评估因子的一个典型流程：

(1) 数据准备

收集资产的收益数据和因子值数据（因子值通常需要标准化）。
确保数据时间对齐（因子值通常是滞后数据，用于预测未来收益）。

(2) 单因子回归

对每个因子单独进行回归：

$r_i = \alpha + \beta F + \epsilon$

检验因子的显著性和解释力。

(3) 多因子回归

同时引入多个因子：

$r_i = \alpha + \beta_1 F_1 + \beta_2 F_2 + \ldots + \beta_k F_k + \epsilon$

测试因子的边际贡献和独立性。

(4) 滚动回归

在时间序列上进行滚动窗口回归（Rolling Regression），检验因子的时间稳定性。
检查回归系数和 $ R^2 $ 是否稳定。

(5) 残差分析

检查残差的分布和序列相关性。
如果残差存在模式（如自相关），可能需要引入其他因子或更复杂的模型。

4. 示例案例

假设你有一个动量因子（过去 12 个月的收益率） $ F_{momentum} $ ，你想评估它的质量：

(1) 单因子回归

对动量因子进行回归：

$r_i = \alpha + \beta_{momentum} F_{momentum} + \epsilon$

如果 $ \beta_{momentum} $ 的 t 值显著，说明动量因子有效。

(2) 多因子回归

加入市值因子（Size）和估值因子（Value）：

$r_i = \alpha + \beta_{momentum} F_{momentum} + \beta_{size} F_{size} + \beta_{value} F_{value} + \epsilon$

检查动量因子是否仍然显著（边际解释力）。
如果动量因子显著但与其他因子相关，可能需要对因子正交化。

(3) 稳定性检验

使用滚动窗口（如 3 个月窗口）回归，查看 $ \beta_{momentum} $ 是否稳定。

5. 注意事项

因子标准化：因子值通常需要 z-score 标准化，以避免量纲问题。
多重共线性：如果多个因子高度相关，可能导致回归结果不稳定，可以考虑主成分分析（PCA）或其他降维方法。
过拟合风险：因子太多或模型复杂可能导致过拟合。

因子与详细解释

1. 什么是因子？

因子的类型

因子可以分为以下几类：

宏观因子：
- 表示市场或经济的整体特征。
- 示例：利率水平、GDP 增速、通胀率。
微观因子：
- 表示单个资产的特性。
- 示例：市值（Size）、账面市值比（Book-to-Market）、动量（Momentum）。
技术因子：
- 从价格、交易量等市场数据衍生的指标。
- 示例：移动平均线、RSI 指标。
风格因子：
- 表示资产所属的某种风格。
- 示例：成长因子（Growth）、价值因子（Value）。

因子的典型数据类型

因子通常是数值型变量，通常在时间和资产的交叉面上定义。它们的数据类型包括：

数值型（连续变量）：例如动量因子（某个时间段内的收益率）。
分类型（离散变量）：例如行业因子（行业分类编码）。

2. 回归方程的含义

回归方程的核心在于表达 资产收益与因子的关系。它试图从数学角度回答以下问题：

收益的驱动力是什么？
哪些因子能够解释收益的变化？
因子的边际贡献如何？

单因子回归方程

单因子回归的形式为：

$r_i = \alpha + \beta F_i + \epsilon$

$ r_i $ ：资产 $ i $ 的收益率，通常是未来某个时间段的收益率。
$ F_i $ ：因子值，代表资产 $ i $ 在某个时间点的特性。
$ \alpha $ ：回归截距，表示在因子对收益没有影响时的收益水平。
$ \beta $ ：回归系数，表示因子值每变化一个单位对资产收益的影响。
$ \epsilon $ ：残差项，表示收益中未被因子解释的部分。

解释：

如果 $ \beta $ 显著为正，说明因子 $ F $ 对资产收益有正向影响。
如果 $ \beta $ 显著为负，说明因子 $ F $ 对资产收益有负向影响。

多因子回归方程

引入多个因子后的回归模型为：

$r_i = \alpha + \beta_1 F_{1i} + \beta_2 F_{2i} + \ldots + \beta_k F_{ki} + \epsilon$

$ F{1i}, F{2i}, \ldots, F_{ki} $ ：表示 $ i $ 资产的不同因子值。
$ \beta_1, \beta_2, \ldots, \beta_k $ ：每个因子的系数，衡量每个因子对收益的边际贡献。

3. 使用回归方程的目的

回归模型在因子分析中的主要应用包括以下几个方面：

(1) 验证因子是否有效

通过回归模型，可以检验因子是否能够显著解释资产收益。如果回归系数（ $ \beta $ ）显著不为零，说明因子对收益有解释力。

目的：判断因子是否有预测能力。

(2) 衡量因子的强弱

回归系数（ $ \beta $ ）的大小表明因子的影响程度。较大的系数表明该因子对收益的影响更强。

目的：筛选强因子。

(3) 分析因子组合的独立性

在多因子模型中，可以检查因子间的独立性。如果两个因子高度相关（共线性），需要进一步处理（如因子正交化）。

目的：提高因子组合的多样性和有效性。

(4) 风险暴露分析

回归模型可以用于分析资产对各个风险因子的暴露程度，从而用于构建风险对冲策略。

目的：管理组合的风险敞口。

(5) 因子投资组合构建

利用因子回归模型，可以根据因子值构建投资组合。例如，买入高因子值资产、卖出低因子值资产，形成因子对冲组合。

目的：构建因子驱动的超额收益策略。

总结

因子是资产收益的驱动变量，而回归模型为我们提供了一种量化分析因子效果的工具。通过回归方程，我们可以：

验证因子的有效性。
衡量因子的强弱。
构建因子组合。
管理风险敞口。

这不仅是评估因子质量的核心步骤，也是将因子应用于投资实践的基础。

ICIR 法

1. ICIR 法的背景与定义

ICIR 法是因子评估和排序的重要方法，主要通过信息系数（IC，Information Coefficient）及其稳定性来衡量因子质量。

IC（Information Coefficient）：衡量因子值与未来收益的相关性。
ICIR（Information Coefficient Information Ratio）：衡量信息系数的稳定性，是 IC 的均值与其波动率的比值。

2. Pearson IC 和 Rank IC 的定义

(1) Pearson IC

Pearson IC 表示因子值和未来收益之间的线性相关性，用 Pearson 相关系数计算：

$IC = \frac{\text{Cov}(F, R)}{\sigma_F \cdot \sigma_R}$

其中：

$ F $ ：因子值（如动量、估值等）。
$ R $ ：未来收益率。
$ \text{Cov}(F, R) $ ：因子值和未来收益之间的协方差。
$ \sigma_F, \sigma_R $ ：因子值和收益率的标准差。

解释：

IC 的取值范围： $ [-1, 1] $ 。
- $ IC > 0 $ ：因子值越大，未来收益越高。
- $ IC < 0 $ ：因子值越大，未来收益越低。
- $ IC \approx 0 $ ：因子值与收益无相关性。
Pearson IC 适用于因子值和收益之间为线性关系的情况。

(2) Rank IC

Rank IC 计算因子值与未来收益的秩相关性，用 Spearman 秩相关系数表示：

$\text{Rank IC} = \text{Spearman Correlation}(Rank(F), Rank(R))$

其中：

$ Rank(F) $ ：因子值的排名。
$ Rank(R) $ ：未来收益的排名。

解释：

Rank IC 不依赖于线性关系，适合因子值和收益之间存在非线性关系的情况。
范围和意义：与 Pearson IC 类似，但更稳健于异常值的影响。

3. 信息比率（IR）的定义

信息比率（IR）用于衡量因子表现的稳定性，定义为 IC 的均值与其标准差的比值：

$IR = \frac{\mathbb{E}[IC]}{\text{Std}(IC)}$

其中：

$ \mathbb{E}[IC] $ ：IC 的平均值。
$ \text{Std}(IC) $ ：IC 的标准差。

解释：

IR 越高，说明因子的表现越稳定。
如果 IR > 1，说明因子有很好的稳定性，投资者可以信任该因子。

4. ICIR 的定义

ICIR 是一种结合因子有效性和稳定性的综合评价指标，定义为：

$ICIR = \frac{\mathbb{E}[IC]}{\text{Std}(IC)}$

ICIR 实际上就是信息比率（IR），它将 IC 的长期均值和波动率结合，反映因子质量的全面性。

5. IC、Rank IC 和 IR 的关系

IC 和 Rank IC：
- Pearson IC 衡量因子值和收益的线性关系。
- Rank IC 衡量因子值和收益的秩序关系（更稳健）。
- 二者的均值可用于衡量因子的整体预测能力。
IC 和 IR：
- IC 衡量因子在单个时间段上的预测效果。
- IR 衡量 IC 的均值与波动率的比值，反映因子在长期上的稳定性。
IC 和 ICIR：
- ICIR 是基于 IC 的稳定性评价，IC 的均值高且波动率低时，ICIR 值会很高。

6. ICIR 法的步骤

(1) 计算 IC 或 Rank IC

在每个时间段计算因子值与未来收益的相关性（可选 Pearson IC 或 Rank IC）。

(2) 计算 IC 的均值和标准差

计算所有时间段 IC 的平均值 $ \mathbb{E}[IC] $ 和标准差 $ \text{Std}(IC) $ 。

(3) 计算 ICIR

$ICIR = \frac{\mathbb{E}[IC]}{\text{Std}(IC)}$

(4) 分析结果

$ ICIR > 1 $ ：因子预测能力强且稳定。
$ 0 < ICIR < 1 $ ：因子预测能力存在，但不稳定。
$ ICIR \leq 0 $ ：因子无效。

7. ICIR 法的意义

因子的有效性评估：
- 高 ICIR 值说明因子不仅预测能力强，而且稳定。
因子优化与筛选：
- 根据 ICIR 排序筛选出高质量因子。
- 优化因子组合时，通过最大化 ICIR 来提升策略性能。
多因子模型的构建：
- 在构建多因子模型时，ICIR 是选择因子的重要参考标准。

总结

IC 衡量因子的预测能力，Rank IC 适合非线性关系。
IR / ICIR 衡量因子表现的稳定性和可靠性。
ICIR 法 是一种结合因子有效性和稳定性的因子评价方法，广泛用于因子筛选、优化和多因子模型的开发。

截面模型

1. 什么是非神经网络类的截面模型？

截面模型用于分析同一时间点下，不同资产的特征（如因子值）与收益之间的关系。这类模型适用于因子分析和选股问题，其中 非神经网络类的模型 通常指机器学习中的传统模型，如树模型、线性模型等。

非神经网络模型的特点：

易于解释：通常具有更高的可解释性。
高效性：在计算资源有限的情况下，比神经网络更快。
灵活性：支持处理非线性关系和高维特征。

2. 树模型概述

树模型是一类基于决策树结构的算法，适合处理非线性特征、特征交互和缺失值。树模型通过逐步分割数据空间来建立预测模型，广泛用于因子分析、收益预测和选股。

决策树基本概念

节点：树的分割点，表示特征值的某个分割阈值。
叶子节点：树的最终输出，通常表示预测值。
树深度：树的层数，表示模型复杂度。

3. 树模型的进阶方法：LightGBM 和 XGBoost

两者是目前量化研究中最常用的树模型，均基于梯度提升决策树（GBDT）框架。

(1) XGBoost

XGBoost (eXtreme Gradient Boosting) 是一种基于梯度提升框架的高效实现，能够处理非线性特征并支持特征重要性分析。

核心思想：通过训练一系列决策树，每一棵树学习前一棵树的残差，从而不断减少预测误差。
主要特性：
- 正则化：在损失函数中加入正则化项，防止过拟合。
- 列采样：在构建树时随机选择部分特征，提高模型的泛化能力。
- 加权分裂：利用信息增益进行更优的特征分割选择。

XGBoost 的公式：

目标函数由两部分组成：

$Obj = L + \Omega$

$ L $ ：训练误差，通常是平方误差或逻辑损失。
$ \Omega $ ：正则化项，防止模型过拟合。

(2) LightGBM

LightGBM (Light Gradient Boosting Machine) 是一种更高效的 GBDT 实现，特别适合处理大规模数据和高维数据。

核心思想：改进了 XGBoost 的算法，采用基于直方图的分裂策略和叶子生长策略。
主要特性：
- 直方图分裂：将连续特征分桶，极大降低了分裂时的计算复杂度。
- 叶子生长：LightGBM 优先扩展损失较大的叶子，而不是逐层生长。
- 支持类别型特征：内置对分类变量的高效处理。

LightGBM 的目标函数：

类似 XGBoost，也由误差项和正则化项组成：

$Obj = L + \Omega$

区别在于：

分裂策略更高效：采用直方图分裂，减少计算。
支持 GPU 加速：在大数据场景中速度更快。

4. 树模型的优势

非线性关系建模：
- 树模型天然支持处理非线性特征关系，适合金融数据中的复杂因子交互。
特征选择与重要性分析：
- 树模型提供特征重要性分析，可以帮助筛选出对收益预测最重要的因子。
鲁棒性：
- 对于异常值和缺失值不敏感，适合处理噪声较大的金融数据。
高效性：
- LightGBM 和 XGBoost 的实现优化使其在大规模数据集上表现出色。

5. 树模型在量化中的应用

因子选取与评估：
- 使用树模型评估因子对收益率的预测能力。
- 分析因子的特征重要性，剔除无效因子。
股票筛选（选股模型）：
- 输入因子特征，输出个股的预测收益率或得分。
- 根据预测结果构建投资组合。
收益预测：
- 使用时间序列数据，预测未来收益分布。
多因子模型优化：
- 使用树模型处理因子非线性关系，实现因子组合的优化。

6. LightGBM 和 XGBoost 的对比

特性	XGBoost	LightGBM
分裂方式	按特征选择最佳分裂点	直方图分裂
生长策略	层级生长	叶子生长
速度	相对较慢	快速（支持 GPU 加速）
内存占用	较高	更低
处理数据类型	需要对类别变量编码	支持原生类别变量
适用场景	中小规模数据，高性能任务	大规模数据，快速迭代

7. 树模型的局限性

解释性：
- 单棵树容易解释，但集成模型（如 XGBoost/LightGBM）因组合了多棵树，解释性较差。
过拟合风险：
- 如果未正确调整超参数（如深度、叶子数），模型可能会过拟合。
时间序列的处理：
- 树模型本质上是截面模型，直接处理时间序列数据时需要特殊处理（如滞后特征）。

8. 实践中的应用建议

特征工程：
- 尽量对因子进行归一化或离散化处理（如分组因子值），以适应模型的输入要求。
超参数调优：
- 对于 XGBoost 和 LightGBM，重点调节以下参数：
  - 树深度（max_depth）
  - 学习率（learning_rate）
  - 子采样比例（subsample）
  - 正则化系数（lambda, alpha）
结合线性模型与树模型：
- 在一些场景中，可以结合线性模型（如线性回归或 LASSO）与树模型的结果，提高因子分析的全面性。

总结来看，LightGBM 和 XGBoost 是强大的非神经网络类截面模型，适用于量化研究中的因子分析和收益预测。它们的非线性建模能力和高效实现使得它们在因子建模、选股和组合构建等任务中表现出色。

时序模型

时序模型的概念

时序模型（Time Series Model）是一类专门用于分析和预测时间序列数据的统计和机器学习模型。这些模型通过捕捉时间序列数据中的趋势、季节性、周期性、以及随机波动等特征，来预测未来的序列值。

时间序列数据的特点

有序性：数据点按照时间顺序排列，顺序不能被打乱。
自相关性：序列中当前时刻的值可能依赖于过去时刻的值。
趋势性：数据可能随时间呈现增长或下降的趋势。
季节性：数据可能周期性波动（如月度销售数据）。

时序模型的分类

时序模型可以分为两大类：统计时序模型 和 机器学习时序模型。

1. 统计时序模型

统计时序模型通过建立明确的数学公式，来解释时间序列的生成过程。这类模型主要依赖假设和参数估计，适合处理线性和规律性较强的数据。

(1) 自回归模型（AR, Autoregressive Model）

描述序列当前值与其 过去的若干滞后值 的线性关系。
模型形式：
- $ X_t $ ：当前时刻的值。
- $ \phi_1, \phi_2, \ldots, \phi_p $ ：自回归系数。
- $ \epsilon_t $ ：误差项。

(2) 移动平均模型（MA, Moving Average Model）

当前值由过去若干 随机误差项的线性组合 决定。
模型形式：
- $ \epsilon_t $ ：白噪声序列。
- $ \theta_1, \theta_2, \ldots, \theta_q $ ：移动平均系数。

(3) ARMA 模型（自回归移动平均模型）

结合了 AR 和 MA 模型，用来描述平稳序列。
模型形式：
$X_t = \phi_1 X_{t-1} + \ldots + \phi_p X_{t-p} + \theta_1 \epsilon_{t-1} + \ldots + \theta_q \epsilon_{t-q} + \epsilon_t$

(4) ARIMA 模型（差分自回归移动平均模型）

适用于非平稳时间序列，通过差分操作使序列平稳。
模型形式：
- $ p $ ：自回归阶数。
- $ d $ ：差分次数。
- $ q $ ：移动平均阶数。

(5) SARIMA 模型（季节性 ARIMA 模型）

考虑季节性因素的 ARIMA 模型。
模型形式：
- $ m $ ：季节性周期。

(6) GARCH 模型（广义自回归条件异方差模型）

描述时间序列波动性随时间变化的模型，广泛用于金融时间序列建模。
模型形式：
- $ h_t $ ：条件方差。

2. 机器学习时序模型

机器学习模型可以通过更灵活的方式捕捉非线性和复杂模式，适用于无明确生成机制的时间序列。

(1) 回归模型

使用回归算法（如线性回归、支持向量机、树模型等）将时间序列的滞后值作为输入，当前值作为输出。

(2) 随机森林与梯度提升树

例如 XGBoost、LightGBM 等可以用来预测时间序列数据，通过构造滞后特征进行预测。
优点：能够捕捉非线性关系。

(3) 长短期记忆网络（LSTM, Long Short-Term Memory）

一种基于 RNN（循环神经网络）的深度学习模型。
通过记忆单元捕捉时间序列的长期依赖关系。
模型形式：
$h_t = f(h_{t-1}, x_t, c_{t-1})$

(4) Transformer 模型

基于注意力机制（Attention），更适合处理长时间序列数据。
在时间序列预测中逐渐流行，例如使用时间嵌入和自回归预测。

(5) Prophet 模型

Facebook 提出的专注于业务场景的时间序列模型。
优点：能够快速建模，捕捉趋势、季节性和节假日效应。

时序模型的应用场景

(1) 金融领域

股票价格预测：捕捉股价变化的趋势和波动。
波动率建模：如 GARCH 模型在期权定价中的应用。
因子收益预测：通过时序模型预测单个因子或多因子的未来表现。

(2) 宏观经济分析

GDP 增速预测、通货膨胀率预测等。

(3) 业务管理

销售预测、库存管理等。

(4) 工业与工程

设备状态监测与故障预测。

时序模型的局限性

假设过强（统计模型）：
- 例如 ARIMA 假设序列是平稳的，而许多实际数据并不满足。
对噪声敏感：
- 特别是统计模型，对异常值和高噪声数据鲁棒性较差。
计算复杂性（机器学习模型）：
- 深度学习模型需要更多的计算资源和数据。
长周期依赖问题：
- 某些模型（如简单 RNN）难以捕捉长期依赖，需要更复杂的模型（如 LSTM 或 Transformer）。

总结

时序模型从简单的统计模型（如 ARIMA、GARCH）到复杂的机器学习模型（如 LSTM、Transformer），都在不同场景中展现了其独特的价值。选择合适的模型应根据数据特性和任务目标：

线性关系、规律性强：优先选择统计模型。
非线性关系、数据复杂：使用机器学习或深度学习模型。

数据源处理

1. 数据源处理的重要性

在量化研究中，数据源的处理是构建有效模型和策略的基础。数据的质量、处理方式和提取的因子直接决定了模型的表现。

核心概念包括：

采样频率：数据记录的时间间隔。
采样时点：数据选取的具体时间点。
因子筛选：从众多变量中选择最有解释力的因子。

2. 采样频率

(1) 定义

采样频率是指数据记录的时间间隔，例如秒级、分钟级、小时级、日级、周级等。不同频率的数据适合不同的研究场景。

(2) 选择采样频率的考虑

策略目标：
- 高频策略：需要秒级或分钟级数据（如高频交易）。
- 中低频策略：常用日级或周级数据（如多因子选股）。
市场特性：
- 高波动市场需要更高频率的数据来捕捉短期变化。
- 稳定市场可用较低频率的数据。
计算资源：
- 高频数据需要更多存储和计算资源，可能会带来过拟合风险。

(3) 常见问题

过采样：
- 采样频率过高会导致过拟合，模型捕捉到噪声而非信号。
欠采样：
- 采样频率过低会丢失关键信息，无法准确反映市场特性。

(4) 处理方法

降频：将高频数据聚合为较低频率数据（如分钟数据转为日数据）。
插值：对低频数据插值，生成高频数据（需谨慎，可能引入偏差）。

3. 采样时点

(1) 定义

采样时点是指数据选取的具体时间点，如日数据中的开盘价、收盘价或某一特定时间的中间价格。

(2) 时点选择的考虑

策略需求：
- 日内策略：需要精确到交易时间的具体点。
- 日间策略：可能选择开盘价或收盘价作为代表。
数据的代表性：
- 收盘价：反映全天交易的最终市场定价，常用于日间策略。
- 开盘价：适合研究市场开盘效应或信息冲击。
- 中间价格（如 VWAP, TWAP）：减少单一时点的极端情况带来的偏差。

(3) 常见问题

跳跃效应：
- 如果仅使用开盘或收盘价，可能会忽略其他时间段的市场波动。
非同步性：
- 跨市场（如股票与期货）数据的时间点不同步会引入噪声。

(4) 处理方法

加权平均：计算加权平均价，如 VWAP（成交量加权平均价）。
同步化：对不同资产的数据进行时间对齐。

4. 因子筛选

(1) 因子的定义

因子是能够解释或预测资产收益的特征变量（如市值、动量、估值等）。

(2) 因子筛选的重要性

在量化研究中，因子库可能包含数百个因子，但并非所有因子都对收益有显著预测力。因子筛选可以：

提升模型效率。
减少冗余，提高解释性。
降低噪声对模型的干扰。

(3) 因子筛选的步骤

1) 数据预处理

标准化：
- 因子值通常需要进行标准化（如 Z-score 转换）以消除量纲差异。
去极值：
- 对因子值的极端值进行处理（如按分位数限制）。
缺失值处理：
- 用均值或中位数填补，或直接删除含缺失值的样本。

2) 初步筛选

经济意义筛选：
- 选择具有明确经济逻辑或理论支持的因子。
- 示例：账面市值比（BM）与估值理论相关。
相关性筛选：
- 剔除与目标收益高度相关或完全无关的因子（如 Pearson 相关系数过低或过高）。
冗余因子剔除：
- 对因子间的相关性进行分析，剔除高度相关（如相关系数 $ >0.8 $ ）的因子。

3) 数量化评估

IC（Information Coefficient）：
- 计算因子值与未来收益的秩相关性，选取 IC 显著的因子。
ICIR（Information Coefficient Information Ratio）：
- 用 IC 的均值除以标准差，选取稳定性较高的因子。
多因子回归：
- 检查因子对收益的边际贡献，剔除无效因子。

4) 迭代优化

交叉验证：
- 验证因子的预测能力是否在不同样本区间内稳定。
主成分分析（PCA）：
- 降维处理，将高度相关的因子合并为主成分。
正则化方法：
- 使用 LASSO 回归自动筛选重要因子。

5. 数据源处理中的注意事项

采样频率与时点的匹配：
- 采样频率和时点应符合策略需求，避免因频率和时点选择不当造成的信号丢失或噪声引入。
因子的经济意义：
- 仅依赖统计筛选可能引入伪因子，因子选择应结合经济学理论或经验逻辑。
多因子组合中的冗余问题：
- 过多的因子可能导致模型复杂度过高或因子间相互干扰。
数据质量控制：
- 确保原始数据没有缺失、错误或异常值，定期验证数据源的可靠性。

总结

数据源处理是量化研究的基石。正确选择采样频率和时点有助于提取有效信号，而因子筛选可以提高模型的效率和预测能力。通过系统化的处理流程，结合经济理论和统计评估，可以为后续模型开发和策略设计提供可靠的数据支持。

模型结构

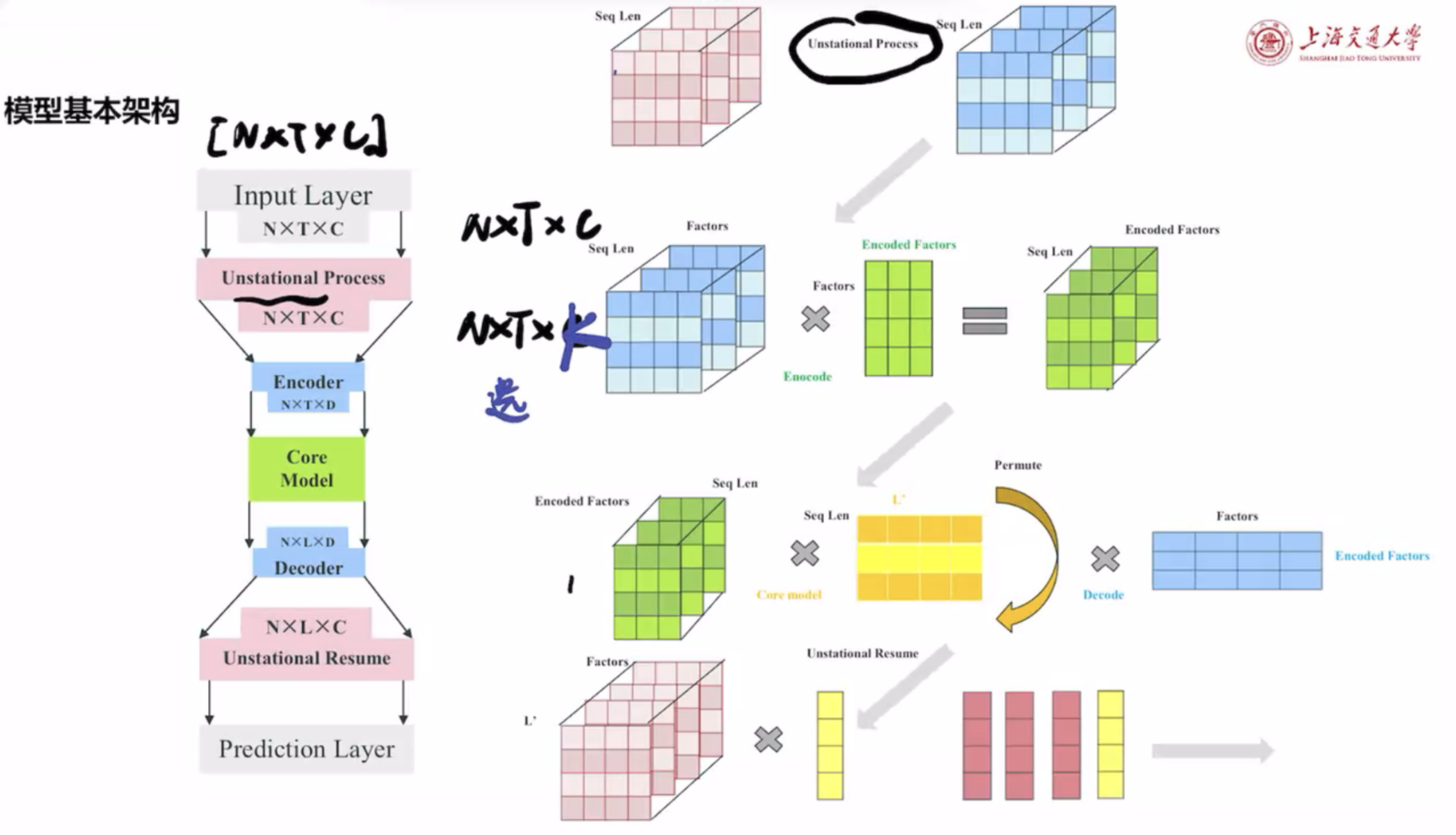
Model-Structure-NTC

这张图展示了一个用于时间序列数据建模的深度学习模型结构，结合了 输入预处理、编码器（Encoder）、核心模型（Core Model）、解码器（Decoder） 和 预测层 的设计。以下是对图中各部分的详细解释：

1. 模型的基本结构

(1) Input Layer

输入形状： $ N \times T \times C $
- $ N $ ：样本数量。
- $ T $ ：时间序列的长度（时间步数）。
- $ C $ ：特征数量（因子数量）。
输入是一个多维张量，表示多个样本在时间序列上的特征。

(2) Unstationary Process（非平稳处理）

目的：对时间序列数据进行非平稳性的预处理。
- 例如：对数据进行归一化、去趋势或对数变换。
- 将输入形状保持为 $ N \times T \times C $ ，但数据可能已被平稳化处理以便更好地输入到模型中。

(3) Encoder

作用：对因子进行编码，将高维原始特征降维或进行特征提取。
输入： $ N \times T \times C $ 。
输出： $ N \times T \times D $
- $ D $ 是编码后的特征维度，通常 $ D \ll C $ 。
如何编码：
- Encoder 可以是一个简单的线性变换（如全连接层）。
- 或者是一个更复杂的模块（如 Transformer 编码器或卷积神经网络）。

(4) Core Model（核心模型）

作用：捕捉时间序列中的动态关系。
输入： $ N \times T \times D $ 。
输出： $ N \times L’ \times D $ 。
- 核心模型将序列长度从 $ T $ 转换为 $ L’ $ ，可能是时间特征的汇总或截断。
可能的实现：
- RNN/LSTM/GRU：捕捉时间序列的长期依赖。
- Transformer：利用注意力机制学习时间序列特征。
- 卷积模型（如 TCN）：提取时间序列的局部模式。

(5) Decoder

作用：将核心模型输出解码为原始维度的特征。
输入： $ N \times L’ \times D $ 。
输出： $ N \times L’ \times C $ 。
如何解码：
- 解码器可以是简单的反向映射（例如通过线性层将维度从 $ D $ 映射回 $ C $ ）。
- 也可以是一个复杂的模块（如多层感知机）。

(6) Unstationary Resume（非平稳恢复）

作用：将经过非平稳处理的数据恢复到原始空间。
- 对预测的输出应用反向操作（例如从归一化恢复到原始尺度）。
输出形状： $ N \times L’ \times C $ 。

(7) Prediction Layer

作用：根据解码后的数据，生成最终的预测值。
可能的目标：
- 回归：预测未来的数值，如资产收益。
- 分类：预测某种类别，如资产涨跌信号。

2. 右侧的分解步骤

右侧部分详细展示了模型中各模块如何操作张量：

(1) 因子的编码过程

输入因子 $ N \times T \times C $ ：
- 通过编码器，将原始高维特征（如价格、成交量等）映射到低维的“编码因子”空间 $ N \times T \times D $ 。

(2) 核心模型的时间特征提取

核心模型（Core Model）：
- 处理时间序列的动态关系。
- 输出的序列可能是长度压缩的 $ L’ $ 。
- 例如：核心模型可能通过卷积或注意力机制提取局部时间模式。

(3) 解码和重构

对核心模型的输出重新解码回原始因子维度 $ C $ ，用于预测任务。

(4) 非平稳性恢复

通过非平稳恢复（Unstationary Resume），将数据映射回原始空间，生成最终的预测。

3. 应用场景

该模型广泛应用于时间序列预测任务，尤其适合以下领域：

量化金融：
- 输入因子数据（如技术指标、基本面数据）。
- 预测资产收益或价格走势。
经济预测：
- 输入宏观经济因子。
- 预测 GDP 增长、通胀等指标。
工业与IoT：
- 输入设备传感器数据。
- 预测设备故障或状态。
自然语言处理（NLP）：
- 输入文本数据（如序列词嵌入）。
- 用于生成或分类任务。

4. 关键技术点

非平稳处理（Unstationary Process）：
- 时间序列往往具有非平稳性（如趋势或季节性），需要通过归一化或去趋势等方法处理。
编码器-解码器结构（Encoder-Decoder）：
- 通过编码器提取特征，核心模型处理动态关系，解码器重构数据。
核心模型的选择：
- RNN/LSTM：适合处理长时间序列。
- Transformer：高效建模长序列，捕捉复杂依赖。
- CNN/TCN：处理短期局部模式。
非平稳恢复（Unstationary Resume）：
- 还原预测结果到原始数据尺度，用于实际应用。

总结

这是一种典型的时间序列深度学习框架，结合了非平稳处理、编码器-解码器结构和时间序列建模技术。通过模块化设计，它能够灵活适应多种时间序列预测任务，特别是在量化金融领域，可以用于因子建模、收益预测或风险评估等。

代码解释

一段基于 PyTorch 的时间序列模型实现，重点是 LSTM 模型的构建。以下对每段代码逐步解释并说明其功能：

1. 第一段代码：`LSTM_Block` 类

代码解析

class LSTM_Block(nn.Module):
    def __init__(self, config):
        super(LSTM_Block, self).__init__()
        self.lstm = nn.LSTM(config.d_model, config.d_model, batch_first=True)

    def forward(self, x):
        lstm_out, _ = self.lstm(x)
        return lstm_out

功能

这是一个 LSTM 模块的封装，用于构建时间序列特征提取的单层 LSTM。
核心组件：
- 使用 nn.LSTM 实现长短期记忆网络（LSTM）。
- 参数说明：
  - config.d_model：输入和输出的隐藏层维度（可能是编码后的特征维度）。
  - batch_first=True：输入数据的维度格式为 (batch_size, seq_len, features)。

`forward` 方法

输入：时间序列数据 $ x $ （维度为 $ N \times T \times C $ ）。
输出：LSTM 的输出 $ lstm_out $ ：
- 形状： $ N \times T \times D $ （与输入形状相同，但经过 LSTM 处理，数据特征可能变化）。

2. 第二段代码：`LSTMModel` 类

代码解析

class LSTMModel(nn.Module):
    def __init__(self, config):
        super(LSTMModel, self).__init__()
        self.config = config
        self.enc_embedding = DataEmbedding(config.c_in, config.d_model, config.dropout)

        # LSTM layers
        lstm_layers = []
        for i in range(config.num_lstm_layer):
            lstm_layers.append(LSTM_Block(config))
            if i != config.num_lstm_layer - 1:
                lstm_layers.append(nn.GELU())  # Non-linear activation
        self.lstm = nn.Sequential(*lstm_layers)

        # Decode layer
        self.projection_layer = nn.Linear(config.d_model, config.c_in)

        # Prediction layer
        self.predict = nn.Sequential(
            nn.Linear(config.c_in, config.pre_len)
        )

功能

这是完整的时间序列预测模型，基于 LSTM 和全连接层构建。

(1) 编码器部分

DataEmbedding：
- 提取输入数据的特征，将 $ C_{in} $ 映射为 $ D $ 维的编码特征。
- 数据经过这个模块后，形状从 $ N \times T \times C_{in} $ 变为 $ N \times T \times D $ 。

(2) 核心部分（LSTM 层）

多层 LSTM 堆叠：
- 通过 LSTM_Block 构建多层 LSTM。
- 如果不是最后一层，LSTM 输出会通过 nn.GELU 激活函数。

(3) 解码部分

self.projection_layer：
- 将 LSTM 的输出特征（ $ D $ 维）映射回原始特征空间 $ C_{in} $ 。
- 解码的输出形状： $ N \times T \times C_{in} $ 。

(4) 预测部分

self.predict：
- 最终的预测层，用全连接层将特征维度 $ C_{in} $ 转换为目标预测长度 pre_len。

3. 第三段代码：`forward` 方法

代码解析

def forward(self, x_enc):
    # Normalization for non-stationary series
    means = x_enc.mean(1, keepdim=True).detach()
    stdev = torch.sqrt(torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5)
    x_enc = (x_enc - means) / stdev

    # Encode
    enc_out = self.enc_embedding(x_enc)

    # Core model part
    lstm_out = self.lstm(enc_out)

    # Decode
    lstm_out = self.projection_layer(lstm_out)

    # Normalization Resume
    lstm_out = lstm_out * (stdev[:, 0, :].unsqueeze(1).repeat(1, lstm_out.size(1), 1))
    lstm_out = lstm_out + (means[:, 0, :].unsqueeze(1).repeat(1, lstm_out.size(1), 1))

    # Prediction
    output = self.predict(lstm_out[:, -1, :])
    return output

功能

这是 LSTMModel 类的前向传播逻辑。分为以下几个阶段：

(1) 数据归一化

通过对输入数据 $ x_enc $ 进行标准化（归一化非平稳序列），确保数据中心化并消除维度间差异：
$x\_enc = \frac{x\_enc - \text{均值}}{\text{标准差}}$
means 和 stdev 分别是按时间维度计算的均值和标准差。

(2) 编码器

输入数据通过 DataEmbedding 提取特征：
- 输入形状： $ N \times T \times C_{in} $ 。
- 输出形状： $ N \times T \times D $ 。

(3) 核心 LSTM 部分

编码后的特征输入多层 LSTM：
- 输入形状： $ N \times T \times D $ 。
- 输出形状： $ N \times T \times D $ 。

(4) 解码器

LSTM 输出通过线性投影，映射回原始特征空间：
- 输入形状： $ N \times T \times D $ 。
- 输出形状： $ N \times T \times C_{in} $ 。

(5) 反归一化

反向恢复数据原始分布：
$\text{lstm\_out} = \text{lstm\_out} \cdot \text{stdev} + \text{means}$

(6) 最终预测

取最后一个时间步的输出 lstm_out[:, -1, :]，通过全连接层得到最终预测值。

4. 代码总结

流程图

输入：时间序列 $ x_enc $ 。
标准化：去除非平稳性。
编码：通过 DataEmbedding 提取特征。
LSTM 核心：通过多层 LSTM 提取时序关系。
解码：将隐藏特征映射回原始空间。
反标准化：恢复到原始数据分布。
预测：生成目标预测值。

创新点

非平稳性处理：标准化和反标准化步骤，有助于应对非平稳序列的噪声和趋势。
模块化设计：
- LSTM_Block 封装了 LSTM，方便构建多层网络。
- DataEmbedding 模块化特征提取。
预测优化：最后时间步的预测使模型更聚焦于未来的预测值。